Linear optimization using Python
Introduction
In this post, I begin by giving a brief description of linear optimization (LO). I
then provide two very basic demonstrations of LO before moving to an empirical
example. I do so
to develop a better understanding of the concepts and the python code to solve LO
problems. Please skip to Question 15.2 if you want to get straight to businness.
In its simplest case, the goal of LO is to maximize or minimize a real function, or the objective function, by systematically choosing a set of input values subject to constraints on the set of values that can be chosen. This case is referred to as LO because the objective function takes the form:
$$ c_1 x_1 + c_2 x_2 +,\dots,c_n x_n $$
for $c_i \in \textbf{R}$ and $c_i = 1,\dots,n$. The constraints, which define the feasible region, take the form:
$$ a_{i1} x_1 + a_{i2} x_2 + \dots + a_{in} x_n \leq b_i \quad i = 1,\dots,s. $$
Example
I demonstrate an LO problem with a simple example. We wish to maximize an objective function of the form:
$$ z = 4x + 5y $$
with three variables $x,y,z$, where we maximize $z$ given the input values $x,y$. We are given two constraints:
$$ \begin{aligned} x + y \leq 20 \ 3x + 4y \leq 72. \end{aligned} $$
We can plot the feasible region by obtaining the $x$ and $y$ values of the two constraints. This is done by setting $x=0$ and $y=0$ for each constraint to find the corresponding coordinate values. For example, in the first constraint, $y = 20$ when $x = 0$. I plot the coordinate pairs and shade the feasible region in blue:
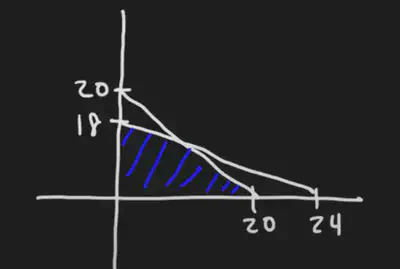
By eyeballing the figure, we can assume that the maximum will be at the point where the
solutions of the two constraints intersect. We can use the pulp package in python to
determine the solution. First, I import pulp and then specify optimization procedure
(LpMaximize).
from pulp import *
op1 = LpProblem("ProblemExample", LpMaximize)
Next I define the $x,y$ variables with values ranging from 0 to 100.
y = LpVariable("y", 0, 100)
x = LpVariable("x", 0, 100)
I then set the constraints:
op1 += x + y <= 20
op1 += 3*x + 4*y <= 72
and set the objective function:
op1 += 4*x + 5*y
We can inspect the setup
print(op1)
ProblemExample:
MAXIMIZE
4*x + 5*y + 0
SUBJECT TO
_C1: x + y <= 20
_C2: 3 x + 4 y <= 72
VARIABLES
x <= 100 Continuous
y <= 100 Continuous
and solve using:
op1.solve()
1
We can find the values of $x,y$ that maximize the objective function:
print(value(x))
8.0
print(value(y))
12.0
Thus, $x=8$ and $y = 12$ are the values that maximize the objective function.
x = 2
x * 38
76
Nutrient data example
In this section I present a simple analysis of some food data. The goal is to find the
cheapest dies that satifies the minimum and maximum nutritional constraints. Here, I
choose Taco and Oatmeal and base the nutrition requirements on protein only. I
begin this exercise with two food items because it is easier to get a grasp of what is
going on in the minimization procedure and the code.
import pandas as pd
dat = pd.read_excel(local_file / "diet.xls", header = 0)
dat
Foods Price/ Serving ... Calcium mg Iron mg
0 Frozen Broccoli 0.16 ... 159.0 2.3
1 Carrots,Raw 0.07 ... 14.9 0.3
2 Celery, Raw 0.04 ... 16.0 0.2
3 Frozen Corn 0.18 ... 3.3 0.3
4 Lettuce,Iceberg,Raw 0.02 ... 3.8 0.1
.. ... ... ... ... ...
62 Crm Mshrm Soup,W/Mlk 0.65 ... 178.6 0.6
63 Beanbacn Soup,W/Watr 0.67 ... 81.0 2.0
64 NaN NaN ... NaN NaN
65 NaN NaN ... 700.0 10.0
66 NaN NaN ... 1500.0 40.0
[67 rows x 14 columns]
From the data, I extract the costs of the two foods and the minimum and maximum nutrient values.
# Select two foods
f2 = ['Taco', 'Oatmeal']
# Select nutrient
n1 = "Protein g"
# Get costs of two foods
costs = dat.loc[dat['Foods'].isin(f2), 'Price/ Serving'].values
costs = {a: b for a,b in zip(f2, costs)}
costs
# Get the nutrients
{'Taco': 0.82, 'Oatmeal': 0.59}
nvals = dat.loc[dat['Foods'].isin(f2), n1].values
nvals = {a: b for a,b in zip(f2, nvals)}
nvals
# get min and max values of nutrient
{'Taco': 6.1, 'Oatmeal': 20.7}
minvals = dat.iloc[65:66][n1].values
maxvals = dat.iloc[66:67][n1].values
minvals; maxvals
array([60.])
array([100.])
We are now ready to setup the variables, constraints, and objective function in pulp.
First, I select the optimization method (LpMinimize) and define the input variables with
minimum values of zero.
# Set env
op2 = LpProblem('Optimization', LpMinimize)
# set the variables
Taco = LpVariable("Taco", 0)
Oatmeal = LpVariable("Oatmeal", 0)
I now define the objective function and constraints using the same method as above.
# Objective function
op2 += costs["Taco"]*Taco + costs["Oatmeal"]*Oatmeal
# Constraints
op2 += nvals['Oatmeal']*Oatmeal >= minvals
op2 += nvals['Oatmeal']*Oatmeal <= maxvals
op2 += nvals['Taco']*Taco >= minvals
op2 += nvals['Taco']*Taco <= maxvals
print(op2)
Optimization:
MINIMIZE
0.59*Oatmeal + 0.82*Taco + 0.0
SUBJECT TO
_C1: 20.7 Oatmeal >= 60
_C2: 20.7 Oatmeal <= 100
_C3: 6.1 Taco >= 60
_C4: 6.1 Taco <= 100
VARIABLES
Oatmeal Continuous
Taco Continuous
I solve and print the values.
op2.solve()
1
oat = value(Oatmeal)
taco = value(Taco)
print(oat)
2.8985507
print(taco)
9.8360656
To minimize costs, 2.9 units of Oatmeal and 9.84 units of Taco are required.
Full analysis
I now minimize the costs for all food items and nutrient requirements. First, I extract the data into the relevant formats.
# Get only the row data
tdat = dat[0:64]
tdat = tdat.values.tolist()
# Get names of foods
fname = [i[0] for i in tdat]
# Get the cost of all foods
cost = dict([(i[0], float(i[1])) for i in tdat])
# Get min/max nutrients
minvals = dat.iloc[65:66, 3:].values
maxvals = dat.iloc[66:67, 3:].values
# Collect the nutrients
nvals = []
for i in range(0,11):
nlist = dict([(j[0], float(j[i+3])) for j in tdat])
nvals.append(nlist)
I now set up the variables, constraints, and objective function, similar to
the earlier nutrient example. This time I will have to loop through the data so that I can
feed it into pulp. In this case the lpSum function is useful.
op3 = LpProblem('Optimize_Foods', LpMinimize)
# Make the variables
fvars = LpVariable.dicts("Var", fname, 0)
# Make obj function
obj_fun = [cost[i] * fvars[i] for i in fname]
op3 += lpSum(obj_fun)
# Constraints
for i in range(0,11):
op3 += lpSum([nvals[i][j] * fvars[j] for j in fname]) >= minvals[0][i]
op3 += lpSum([nvals[i][j] * fvars[j] for j in fname]) <= maxvals[0][i]
Now I run the solver and print out the results, which shows the units needed for the following foods to reduce cost (subject to nutrient constraints). I also show the total cost per meal serving.
op3.solve()
# The units of food items required
1
for nm in op3.variables():
if value(nm) > 0:
print(str(nm) + " " + str(round(value(nm), 2)) + " units required")
# The cost per ingredients for each serving
Var_Celery,_Raw 52.64 units required
Var_Frozen_Broccoli 0.26 units required
Var_Lettuce,Iceberg,Raw 63.99 units required
Var_Oranges 2.29 units required
Var_Poached_Eggs 0.14 units required
Var_Popcorn,Air_Popped 13.87 units required
print("Total Cost of Ingredients per serving = ", round(value(op3.objective), 2))
Total Cost of Ingredients per serving = 4.34
